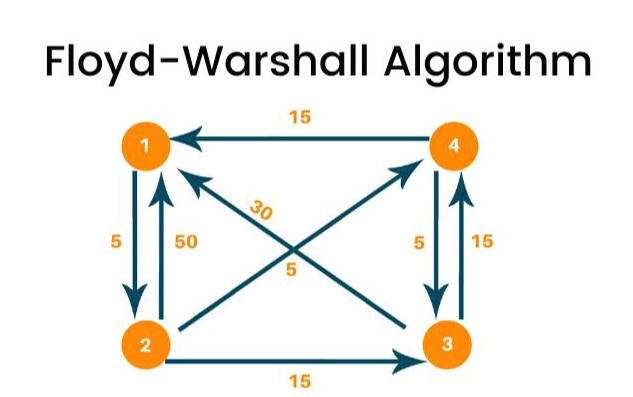
플로이드 워셜 알고리즘(Floyd-Warshall Algorithm)은 '모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우'에 사용할 수 있는 알고리즘이다. '한 지점에서 다른 특정 지점까지의 최단 경로를 구해야 하는 경우'에 사용할 수 있는 다익스트라 최단 경로 알고리즘과 이 부분에서 차이가 있다. 플로이드 워셜 알고리즘의 소스코드는 매우 짧아서 다익스트라 알고리즘과 비교하면 구현 과정에서 어려움을 겪지는 않을 것이다. 다만, 핵심 아이디어를 이해하는 것이 중요하다.
다익스트라 알고리즘은 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다. 그리고 해당 노드를 거쳐 가는 경로를 확인하며, 최단 거리 테이블을 갱신하는 방식으로 동작한다. 플로이드 워셜 알고리즘 또한 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다. 하지만 매번 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다는 점이 다르다. 노드의 개수가 N개일 때 알고리즘상으로 N번의 단계를 수행하며, 단계마다 O(N^2)의 연산을 통해 '현재 노드를 거쳐 가는' 모든 경로를 고려한다. 따라서 플로이드 워셜 알고리즘의 총시간 복잡도는 O(N^3)이다.
다익스트라 알고리즘에서는 출발 노드가 1개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해서 1차원 리스트를 이용했다. 반면에 플로이드 워셜 알고리즘은 다익스트라 알고리즘과는 다르게 2차원 리스트에 '최단 거리' 정보를 저장한다는 특징이 있다. 모든 노드에 대하여 다른 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문이다. 다시 말해 2차원 리스트를 처리해야 하므로 N번의 단계에서 매번 O(N^2)의 시간이 소요된다.
또한 다익스트라 알고리즘은 그리디 알고리즘인데 플로이드 워셜 알고리즘은 다이나믹 프로그래밍이라는 특징이 있다. 노드의 개수가 N이라고 할 때, N번 만큼의 단계를 반복하며 '점화식에 맞게' 2차원 리스트를 갱신하기 때문에 다이나믹 프로그래밍으로 볼 수 있다.
각 단계에서는 해당 노드를 거쳐 가는 경우를 고려한다. 예를 들어 1번 노드에 대해서 확인할 때는 1번 노드를 중간에 거쳐 지나가는 모든 경우를 고려하면 된다. 정확히는 A → 1번 노드 → B로 가는 비용을 확인한 후에 최단 거리를 갱신한다. 이를테면 현재 최단 거리 테이블에 A번 노드에서 B번 노드로 이동하는 비용이 3으로 기록되어 있을 때, A번 노드에서 1번 노드를 거쳐 B번 노드로 이동하는 비용이 2라는 것이 밝혀지면, A번 노드에서 B번 노드로 이동하는 비용을 2로 갱신하는 것이다.
따라서 알고리즘에서는 현재 확인하고 있는 노드를 제외하고, N - 1개의 노드 중에서 서로 다른 노드 (A, B)쌍을 선택한다. 이후에 A → 1번 노드 → B로 가는 비용을 확인한 뒤에 최단 거리를 갱신한다. 다시 말해 [N-1]P[2]개의 쌍을 단계마다 반복해서 확인하면 된다. 이때 O([N-1]P[2])는 O(N^2)이라고 볼 수 있기 때문에, 전체 시간 복잡도는 O(N^3)이라고 할 수 있다. 구체적인 (K번의 단계에 대한) 점화식은 다음과 같다.
D[ab] = min(D[ab], D[ak] + D[kb])
따라서 전체적으로 3중 반복문을 이용하여 이 점화식에 따라 최단 거리 테이블을 갱신하면 된다. 위의 점화식이 의미하는 내용을 말로 풀어 설명하자면, 'A에서 B로 가는 최소 비용'과 'A에서 K를 거쳐 B로 가는 비용'을 비교하여 더 작은 값으로 갱신하겠다는 것이다. 즉, '바로 이동하는 거리'가 '특정한 노드를 거쳐서 이동하는 거리'보다 더 많은 비용을 가진다면 이를 더 짧은 것으로 갱신한다는 것이다. 다음 그림을 통해서 구체적인 예시를 확인해보도록 하자.

이런 그래프가 있을 때, 우리는 다음처럼 초기 테이블을 설정할 수 있다. 초기 상태인 [step 0]에서는 '연결된 간선'은 단순히 그 값을 채워 넣고, 연결되지 않은 간선은 '무한'이라는 값을 넣는다. 마찬가지로 실제 구현에서는 10억과 같은 임의의 큰 값을 '무한'이라고 여기고 넣는다. 앞서 다익스트라에서와 마찬가지로 파이썬에서는 int(1e9)를 이용하는 것이 일반적이다. 2차원 리스트에서 각 값에 해당하는 D[ab]는 'a에서 b로 가는 최단 거리'이다.
예를 들어 1번 노드에서 4번 노드로 가는 비용은 6이기 때문에 다음의 2차원 리스트의 첫 번째 행의 네 번째 열의 값이 6인 것을 확인할 수 있다. 그리고 자기 자신에서 자기 자신으로 가는 비용은 0이므로, (1 ≤ i ≤ n)의 범위를 가지는 모든 i에 대하여 D[ii]는 0이라는 값으로 초기화 한다. 즉, 왼쪽 위에서 오른쪽 아래로 내려가는 대각선에 놓인 모든 원소는 0이다.
step 0.
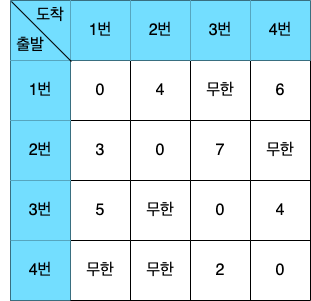
step 1. [step 1]에서는 단순히 1번 노드를 거쳐 가는 경우를 고려한다. 이때는 정확히 다음과 같이 6 = [3]P[2]가지 경우에 대해서만 고민하면 된다. 2차원 테이블에서는 다른 색으로 칠해 놓았는데, 계산해야 할 값들은 구체적으로 다음과 같다.
D[23] = min(D[23], D[21] + D[13])
D[24] = min(D[24], D[21] + D[14])
D[32] = min(D[32], D[31] + D[12])
D[34] = min(D[34], D[31] + D[14])
D[42] = min(D[42], D[41] + D[12])
D[43] = min(D[43], D[41] + D[13])
이 6가지 경우만 하나씩 확인하며 값을 계산하여 갱신한다. 예를 들어 D[23] = min(D[23], D[21] + D[13])은 '기존의 2번 노드에서 3번 노드로 가는 비용'보다 '2번 노드에서 1번 노드를 거쳐 3번 노드로 가는 비용'이 더 작다면, 그것으로 갱신해주겠다는 의미를 가진다. 그래서 D[23]의 값은 D[23]과 (D[21] + D[13]) 중에서 더 작은 값으로 교체된다. 다시 말해 1을 거쳐 갈 때가 더 빠른 경우가 존재한다면 빠른 경우로 최단 거리를 갱신해주는 식이다.

이렇게 6가지 식을 모두 계산해서 값을 갱신하면 테이블이 다음과 같이 바뀐다. 예를 들어 D[24]는 원래 '무한'의 값을 가졌는데, D[21] + D[14] = 9와 비교해서 9로 갱신된다.
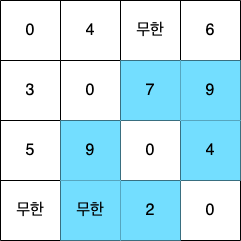
step 2. 마찬가지로 알고리즘을 [step 2]에 대해서도 수행할 수 있다. 현재 테이블의 상태는 다음과 같다.

이번에는 2번 노드를 거쳐 가는 경우를 계산해야 하므로 2번 노드를 제외한 1번, 3번, 4번 노드에서 2개의 노드를 뽑는 경우를 고려한다. 정확히 (1, 3), (1, 4), (3, 1), (3, 4), (4, 1), (4, 3)으로 6가지 경우가 있다. 각각의 위치를 테이블 상에서 하늘색으로 표시하면 다음과 같다. 이 6가지 값만 갱신하면 된다.
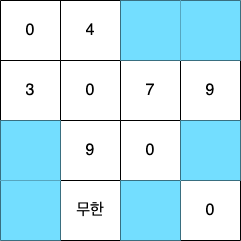
마찬가지로 하늘색 부분에 대해서만 고려하면, 갱신 결과는 다음과 같다. 예를 들어 D[13]은 원래 '무한'의 값을 가졌는데, D[12] + D[23] = 11과 비교해서 11로 갱신된다.

step 3. 마찬가지로 3번 노드에 대해서도 동일한 과정을 반복하면 된다. 현재 테이블은 다음과 같은 값을 가지고 있다.

3번을 제외하고 1번, 2번, 4번 중에서 두 쌍을 선택하는 경우는 (1, 2), (1, 4), (2, 1), (2, 4), (4, 1), (4, 2)로 6가지 경우가 있다. 이 6가지 경우를 색칠하면 다음과 같다.
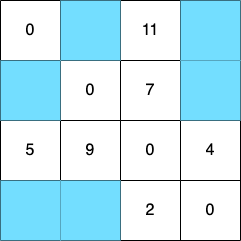
마찬가지로 [step 3]에 대해서도 점화식에 맞게 테이블을 갱신하여, 변경된 결과를 확인하면 다음과 같다.
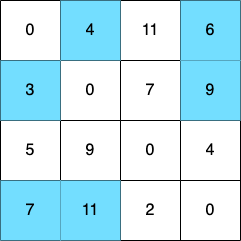
step 4. 마찬가지로 4번 노드에 대해서도 처리할 수 있다. 현재 테이블의 상태는 다음과 같다.

4번 노드를 거쳐 가는 경우를 고려하면 다음과 같이 6가지 경우를 테이블에 색칠해두었다.
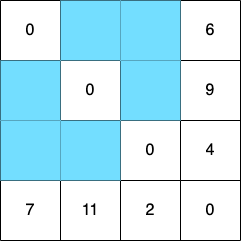
갱신된 결과는 다음과 같다.

최종 결과
노드의 개수가 4개이므로 총 [step 4]까지 알고리즘을 수행하였다. 그래서 [step 4]가 모두 수행되었을 때 최종적으로 테이블의 형태는 다음과 같다. 여기 기록되어 있는 내용이 모든 노드에서 모든 노드로 가는 최단 거리 정보를 표현하고 있다. 예를 들어 D[13](첫 번째 행의 세 번째 열)은 8이라는 값을 가지고 있는데, 이는 1번 노드에서 3번 노드로 가는 최단 거리가 8이라는 의미다.
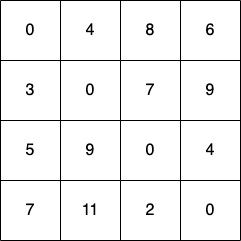
소스코드는 다음과 같다. 시간 복잡도는 O(N^3)이다.
INF = int(1e9) # 무한을 의미하는 값으로 10억을 생성
# 노드의 개수 및 간선의 개수를 입력 받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0
# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
# A에서 B로 가는 비용은 C라고 설정
a, b, c = map(int, input().split())
graph[a][b] = c
# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 수행된 결과를 출력
for a in range(1, n + 1):
for b in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if graph[a][b] == INF:
print("INFINITY", end=' ')
# 도달할 수 있는 경우 거리를 출력
else:
print(graph[a][b], end=' ')
print()
나동빈, 2021, 「이것이 취업을 위한 코딩 테스트다 with 파이썬」, 한빛미디어.
'Data Structure & Algorithm' 카테고리의 다른 글
| 서로소 집합 알고리즘(Disjoint Sets Algorithm) - 그래프 이론 (0) | 2022.05.17 |
|---|---|
| 그래프 이론 (0) | 2022.05.17 |
| 다익스트라(Dijkstra) 최단 경로 알고리즘 (0) | 2022.05.15 |
| 다이나믹 프로그래밍(Dynamic Programming) (0) | 2022.05.13 |
| 이진 탐색(Binary Search) 알고리즘 (0) | 2022.05.12 |



